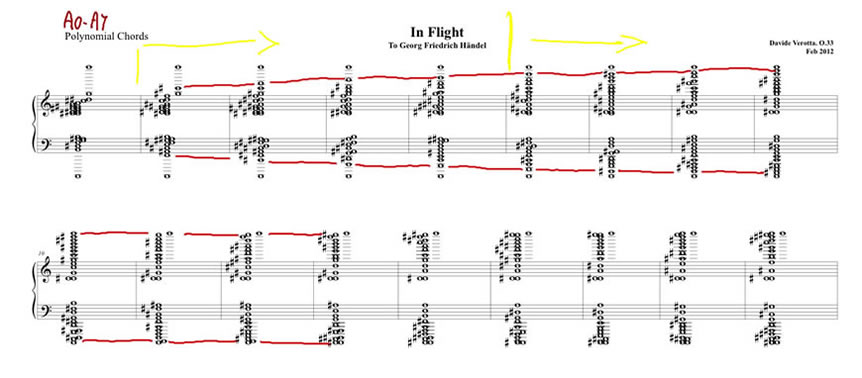
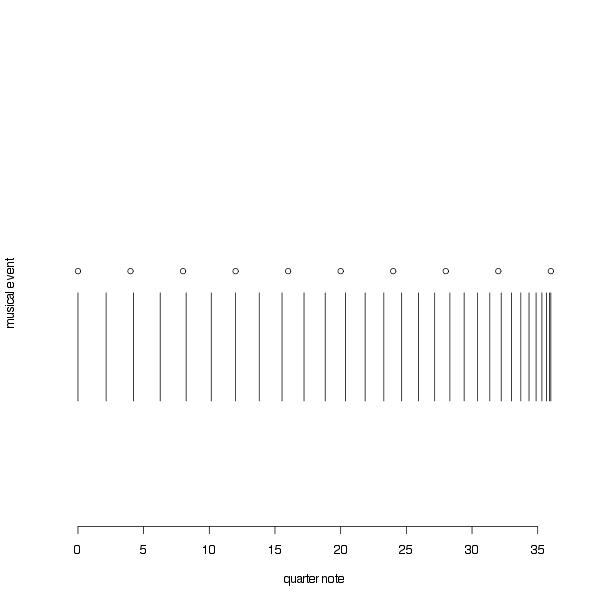
Second, an approach used in Midday, where I use two chords derived from inharmonic series (obtained by altering the harmonic series using a relationship between the fundamental and the harmonics that grows slower than linearly).

The chords are obtained using n=11 (left) and n=12 (right) harmonics. The parameter $\gamma$ determines the rate of growth of the inharmonic series. The value of dissonance reported in the figure is for reference only. Midday is a piece for wind quintet, characterized by un ascent from the lowest to the highest pitches of the two chords. Because there are only five possible voices the chords as depicted are never heard in their entirety in the piece. Under each chord are also reported the scales that can are obtained from the corresponding series. The scales are used during the "ascent" that takes place in the piece.

In Ultramarinus for orchestra I use again inharmonic series, but I also include their transpositions.

In the same piece I occasionally use accellerandos obtained using a simple power law. The accelerandos take forms as in the figure below, where a vertical bar indicates a musical event (e.g. a new pitch) and the open circles mark the measure bar. Thepower law is simply: Time of Event $= n x^\gamma$ where $n$, in this case, is the number of quater notes, $x$ an equispaced sequence with length equal to the total number of events, $x \in [0,1]$, $\gamma$ is a parameter that determines the rate of acceleration. When $\gamma = 1$ we obtain (metric) events spaced at quarter notes.